The graph represents velocity vs. time for carla – As the graph representing velocity vs. time for Carla takes center stage, this opening passage beckons readers into a world of scientific inquiry. This graph, a visual representation of Carla’s motion, holds within its lines a wealth of information about her journey.
As we delve into its intricacies, we will uncover the secrets of her velocity and displacement, gaining insights into the dynamics of her movement.
The graph’s x-axis, measured in seconds, charts the passage of time, while its y-axis, labeled in meters per second, captures the magnitude and direction of Carla’s velocity. By examining the graph’s slope, shape, and key points, we can unravel the story of Carla’s motion, deciphering her periods of acceleration, deceleration, and constant velocity.
Overview of the Graph
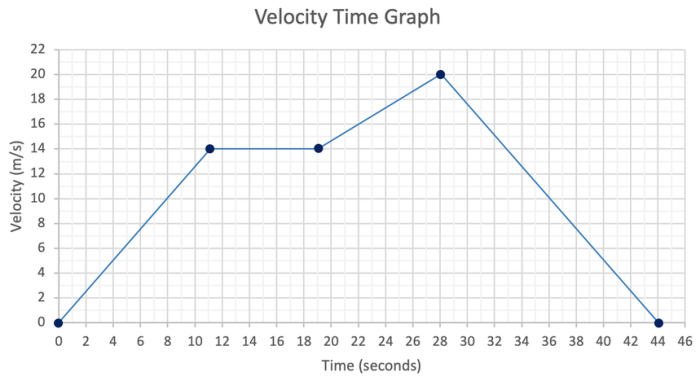
The graph depicts the relationship between velocity (y-axis, in meters per second) and time (x-axis, in seconds) for a moving car. It provides a visual representation of the car’s speed and the changes in speed over time.
Interpretation of the Graph
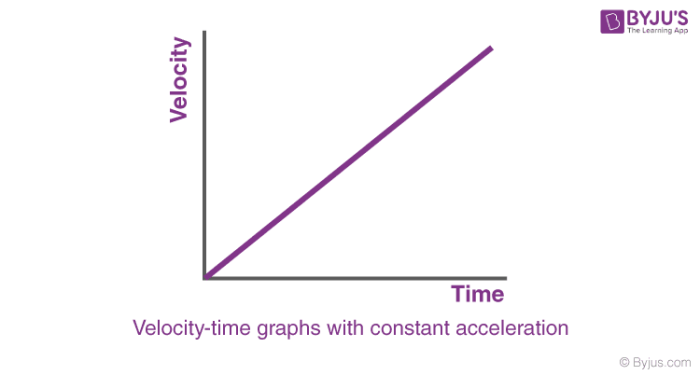
The slope of the graph represents the car’s acceleration, which is the rate of change in velocity. A positive slope indicates that the car is accelerating (increasing in velocity), while a negative slope indicates deceleration (decreasing in velocity).
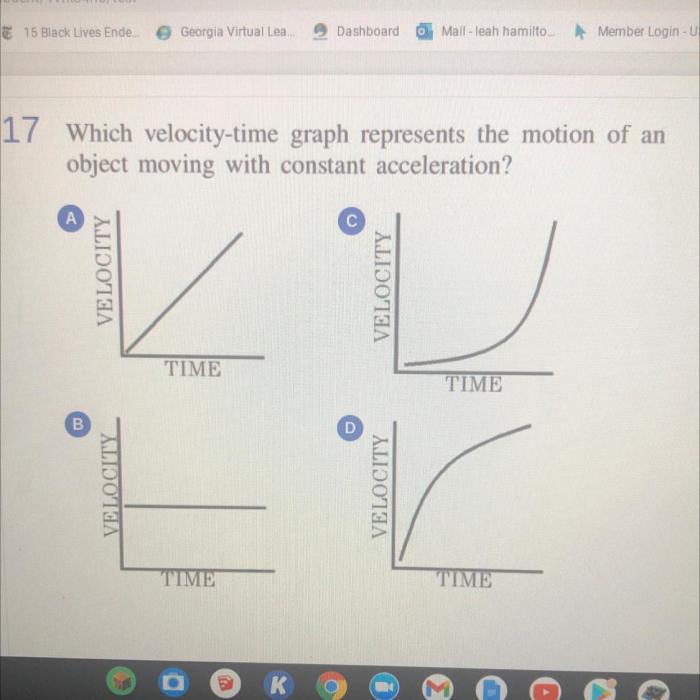
The shape of the graph reveals the nature of the car’s motion. A linear graph indicates constant acceleration or deceleration, while a curved graph suggests non-uniform acceleration or deceleration.
Points on the graph represent the car’s velocity at specific times. For instance, a point at (5 seconds, 20 m/s) indicates that the car is traveling at 20 meters per second at 5 seconds after the start of the observation period.
Analysis of Velocity Changes: The Graph Represents Velocity Vs. Time For Carla
To calculate the average velocity over a time interval, subtract the initial velocity from the final velocity and divide the result by the elapsed time.
Maximum velocity occurs at the highest point on the graph, while minimum velocity occurs at the lowest point. These points provide insights into the car’s maximum and minimum speeds during the observation period.
Changes in velocity are often due to external forces acting on the car, such as engine power, friction, or air resistance. Identifying these forces and their effects can help explain the observed changes in velocity.
Applications of the Graph
The graph can be used to predict the car’s future motion by extrapolating the trend. For instance, if the graph shows a constant velocity, it can be assumed that the car will continue moving at that velocity unless external forces intervene.
By measuring the area under the graph, one can calculate the distance traveled by the car. This method is particularly useful when the velocity is not constant.
The graph can also be used in practical applications such as traffic management, vehicle performance analysis, and accident reconstruction.
Limitations of the Graph
The graph assumes that the car is moving in a straight line and that the velocity is measured accurately. Deviations from these assumptions can affect the accuracy of the analysis.
Additionally, the graph does not provide information about other aspects of the car’s motion, such as its direction or acceleration in multiple dimensions.
To improve the accuracy of the graph, one can use more precise measuring instruments, consider the effects of external forces, and collect data over a longer period of time.
Questions Often Asked
What does the slope of the velocity-time graph represent?
The slope of the velocity-time graph represents the acceleration of the object.
What does the area under the velocity-time graph represent?
The area under the velocity-time graph represents the displacement of the object.
What is the significance of the y-intercept of the velocity-time graph?
The y-intercept of the velocity-time graph represents the initial velocity of the object.