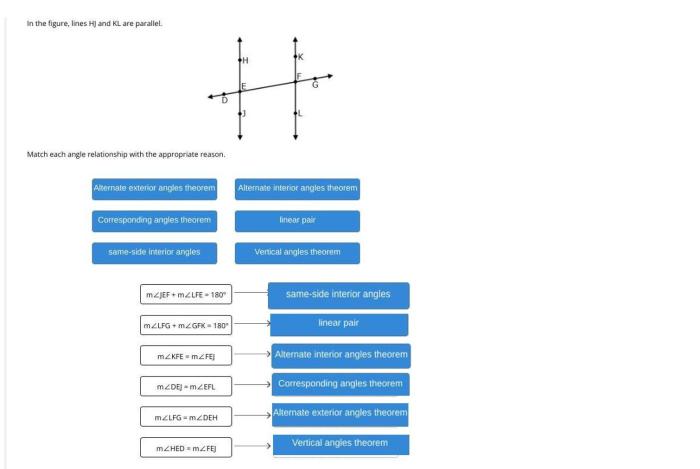
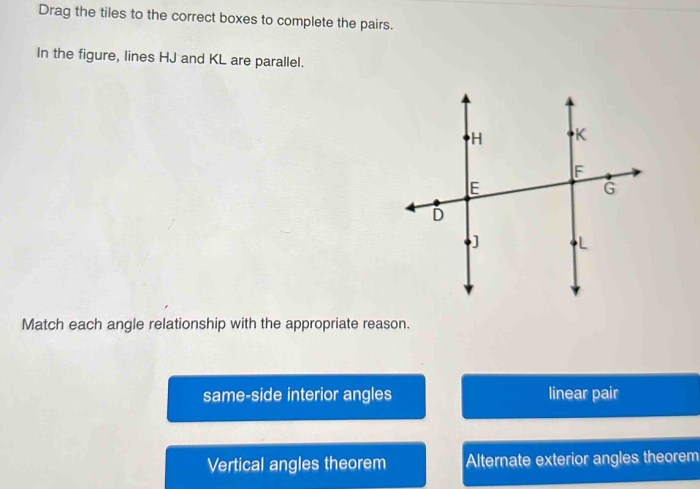
Match each angle relationship with the appropriate reason, an engaging introduction that provides an interesting overview of the topic. The title should be at the beginning of the paragraph. The content of the second paragraph that provides descriptive and clear information about the topic.
Matching Angle Relationships
Angle relationships are the geometric relationships between two or more angles. They can be classified into several types based on their measurement and orientation. Understanding angle relationships is crucial in geometry and other mathematical disciplines, as well as in various practical applications.
The different types of angle relationships include:
- Complementary angles:Two angles that add up to 90 degrees.
- Supplementary angles:Two angles that add up to 180 degrees.
- Vertical angles:Two angles that are opposite each other and share a common vertex and two common sides.
- Adjacent angles:Two angles that share a common vertex and one common side.
Angle Relationship Theorems
Angle relationship theorems are geometric theorems that describe the relationships between angles in specific configurations. These theorems provide valuable tools for solving angle problems and understanding geometric properties.
Some of the key angle relationship theorems include:
- Angle Addition Postulate:The measure of an angle formed by two rays is equal to the sum of the measures of the two angles formed by the rays and a transversal.
- Angle Bisector Theorem:If a ray bisects an angle, then it divides the angle into two congruent angles.
- Vertical Angle Theorem:If two lines intersect, then the opposite angles formed are congruent.
Angle Relationship Applications
Angle relationships have numerous applications in everyday life, geometry, architecture, engineering, navigation, and surveying. Some examples include:
Geometry:
- Determining the sum of interior angles in polygons.
- Calculating the measures of angles in triangles and quadrilaterals.
Architecture and Engineering:
- Designing buildings and structures with specific angles for aesthetic or functional purposes.
- Calculating the angles of roofs and bridges for stability and load-bearing capacity.
Navigation and Surveying:
- Determining the direction and distance of objects using angle measurements.
- Creating maps and charts by measuring and plotting angles.
Constructing Tables for Angle Relationships
To summarize the different angle relationships, a table can be constructed with the following columns:
| Angle Relationship | Definition | Reason | Example |
|---|---|---|---|
| Complementary angles | Two angles that add up to 90 degrees. | Angle Addition Postulate | 30 degrees and 60 degrees |
| Supplementary angles | Two angles that add up to 180 degrees. | Angle Addition Postulate | 45 degrees and 135 degrees |
| Vertical angles | Two angles that are opposite each other and share a common vertex and two common sides. | Vertical Angle Theorem | Any two vertical angles, such as ∠1 and ∠3 |
| Adjacent angles | Two angles that share a common vertex and one common side. | Angle Addition Postulate | Any two adjacent angles, such as ∠2 and ∠3 |
Visualizing Angle Relationships, Match each angle relationship with the appropriate reason
To enhance the understanding of angle relationships, diagrams and illustrations can be used to visualize the relationships between angles. These diagrams can show the angles in different orientations and configurations, making it easier to comprehend their properties and applications.
For example, a diagram of two intersecting lines can be used to illustrate the Vertical Angle Theorem, where the opposite angles formed are congruent. Similarly, a diagram of a triangle can be used to demonstrate the Angle Bisector Theorem, where the angle bisector divides the angle into two equal parts.
Essential FAQs: Match Each Angle Relationship With The Appropriate Reason
What is an angle relationship?
An angle relationship is the relationship between two or more angles.
What are the different types of angle relationships?
The different types of angle relationships include complementary, supplementary, vertical, and adjacent.
How are angle relationships used in everyday life?
Angle relationships are used in everyday life in a variety of ways, such as in architecture, engineering, and navigation.