Embark on a mathematical expedition with our “Characteristics of Exponential Functions Worksheet,” where we delve into the fascinating world of exponential functions, their unique properties, and their ubiquitous applications in real-world phenomena.
Exponential functions, defined by their distinctive form (y = a^x), exhibit remarkable characteristics, including rapid growth and one-to-one relationships. We will explore these properties, uncover their implications, and witness how exponential functions model a myriad of natural and man-made occurrences.
1. Exponential Functions
An Overview
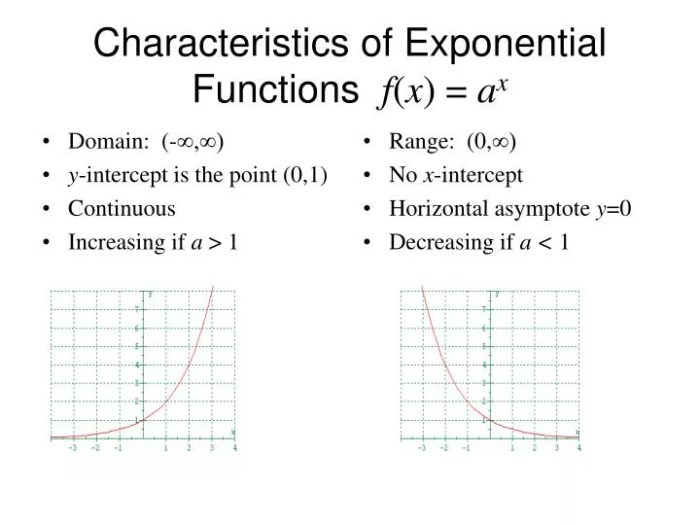
Exponential functions are a class of mathematical functions that exhibit rapid growth or decay. They are commonly used to model phenomena where the rate of change is proportional to the current value. The general form of an exponential function is y = a^x, where a is the base and x is the exponent.
Key characteristics of exponential functions include:
- Rapid growth or decay: The value of y increases or decreases rapidly as x increases.
- One-to-one relationship: Each value of x corresponds to a unique value of y.
Exponential functions are found in various real-world contexts, such as population growth, radioactive decay, and compound interest.
2. The Graph of an Exponential Function
To graph an exponential function using the general form y = a^x, follow these steps:
- Plot the point (0, 1) on the y-axis, which represents the initial value.
- Use the base a to determine the direction of the graph. If a > 1, the graph rises; if a< 1, the graph falls.
- Plot additional points by multiplying the previous y-value by the base a.
- Connect the points with a smooth curve.
Key features of the graph of an exponential function include:
- Asymptote: The line y = 0 is a horizontal asymptote, which the graph approaches but never touches.
- Intercepts: The graph intercepts the y-axis at (0, 1) and the x-axis at (1, a).
- Shape: The graph is either concave up (a > 1) or concave down (a< 1).
3. Transformations of Exponential Functions
Exponential functions can be transformed by translating, reflecting, and stretching.
Translation
To translate an exponential function y = a^x vertically by k units, use the function y = a^(x + k). To translate horizontally by h units, use y = a^(x – h).
Reflection, Characteristics of exponential functions worksheet
To reflect an exponential function y = a^x over the x-axis, use the function y = -a^x. To reflect over the y-axis, use y = a^(-x).
Stretching
To stretch an exponential function y = a^x vertically by a factor of b, use the function y = (ba)^x. To stretch horizontally by a factor of c, use y = a^(cx).
The following table summarizes the transformations and their effects on the graph:
| Transformation | Function | Effect on Graph |
|---|---|---|
| Vertical translation up by k units | y = a^(x + k) | Shifts the graph up by k units |
| Vertical translation down by k units | y = a^(x
|
Shifts the graph down by k units |
| Horizontal translation right by h units | y = a^(x
|
Shifts the graph right by h units |
| Horizontal translation left by h units | y = a^(x + h) | Shifts the graph left by h units |
| Reflection over the x-axis | y =
|
Flips the graph over the x-axis |
| Reflection over the y-axis | y = a^(-x) | Flips the graph over the y-axis |
| Vertical stretch by a factor of b | y = (ba)^x | Stretches the graph vertically by a factor of b |
| Vertical compression by a factor of b | y = (a/b)^x | Compresses the graph vertically by a factor of b |
| Horizontal stretch by a factor of c | y = a^(cx) | Stretches the graph horizontally by a factor of c |
| Horizontal compression by a factor of c | y = a^(x/c) | Compresses the graph horizontally by a factor of c |
4. Applications of Exponential Functions
Exponential functions are widely used to model real-world phenomena, including:
- Population growth: The exponential function y = a(1 + r)^t models population growth, where a is the initial population, r is the growth rate, and t is the time.
- Radioactive decay: The exponential function y = a(1/2)^(t/h) models radioactive decay, where a is the initial amount of radioactive substance, h is the half-life, and t is the time.
- Compound interest: The exponential function y = P(1 + r/n)^(nt) models compound interest, where P is the principal, r is the annual interest rate, n is the number of times per year interest is compounded, and t is the time.
Exponential functions can be used to solve problems in these contexts. However, it is important to note that exponential models may not always be appropriate, especially when the rate of change is not constant or when there are other factors that affect the phenomenon being modeled.
Detailed FAQs: Characteristics Of Exponential Functions Worksheet
What is the general form of an exponential function?
y = a^x, where a is the base and x is the exponent.
What is a key characteristic of exponential functions?
Rapid growth, where the function increases rapidly as the exponent increases.
Can exponential functions be transformed?
Yes, they can be translated, reflected, and stretched using specific rules.
What are some real-world applications of exponential functions?
Modeling population growth, radioactive decay, and compound interest.